DQN 系列算法-DQN 进化之路
本篇介绍基于价值的深度强化学习算法 DQN 与该系列算法的不断改进之路。
Double-DQN
- 目的:解决基础 DQN 算法系统性高估 Q 值问题。
问题说明:
基础 DQN 会维护两个网络,Local_Network 和 Target_Network。Local_Network: 用于选择估值最高的动作 aTarget_Network: 用于估计做出动作 a 之后总回报。
最基础的 DQN 会根据这两个网络计算 “期望 Q 值” 和 “目标 Q 值”,不断优化网络参数缩小这两个 Q 值之间的差距。
DQN 网络更新流程如下:
- 计算期望 Q 值:\(Q_e \approx Q_{local}(s_{t},a_{t};local)\)(根据当前游戏环境状态和当前本地网络选择的动作 a 条件下的未来总回报的期望)
- 计算目标 Q 值:\(Q_t \approx r_t + \gamma \cdot Q_{target}(s_{t+1},a_{t+1};target)\)(当前动作的奖励 + 目标网络对的$s_{t+1}$状态下做出最好的动作$a_{t+1}$后未来总回报的估计值)
更新 Loss(期望Q, 目标Q)
同步两个网络
Local_Network和Target_Network的参数。
DQN 算法存在的问题:
在计算目标 $Q$ 值这一步中,在取得 $t+1$ 时刻的未来总回报估计值 $Q_{target}(s_{t+1},a_{t+1};target)$时,实际上通过 Target Network 做了两件事
动作选择 和 价值估计 该网络选择了它认为的最好动作$a_{t+1}$并且评估了做出$a_{t+1}$后得到的未来总回报。
$$Q_{target}(s_{t+1},a_{t+1};target) = \max[Q_{target}(s_{t+1},a_{1}),Q_{target}(s_{t+1},a_{2}),…Q_{target}(s_{t+1},a_{n})]$$ 这种做法会导致对动作 Q 值的高估。
Q 值高估
- 如果目标网络选择了错误的动作,则说明对该动作的 Q 值评估存在高估
- 并且随着动作空间增加这种高估现象会更加明显
- 如果游戏环境复杂,动作空间与状态空间非常大,智能体没能充分探索所有的(动作,状态)那么Q的高估对导致智能无法做出最优动作,而是选择次优动作或错误动作。
Double DQN 算法解决方法:
通过把 动作选择 和 价值估计 两步骤解耦,通过 Local_Network 选择动作, Target_Network 进行价值估计,来减小 Q 值估计的偏差。
Double-DQN 网络区别:
计算期望 Q 值:$Q_{expected} \approx Q_{local}(s_{t},a_{t};local)$ (不变)
计算目标 Q 值:
$a_{t+1} = Q_{local}(s_{t+1})$(动作是从 local 网络中选择)
$Q_{target} \approx r_t + \gamma \cdot Q_{target}(s_{t+1},a_{t+1};target)$
总结
- Double DQN 对 Q 值的估计比传统 DQN 更加保守
- Double DQN 在处理高偏差方面取得了比较好的效果,适合于较大的动作空间与状态空间
PRE-DQN (优先经验回放)
基础 DQN 经验回放:
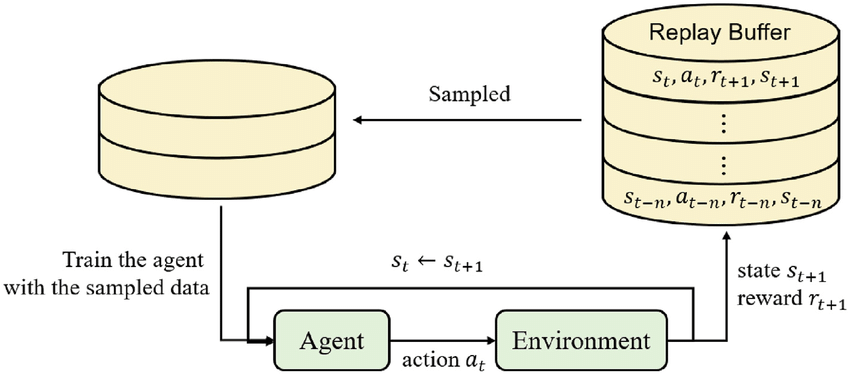
- 将模型与环境交互得到的轨迹 ($s_{t}$, $a_{t}$, $r_{t}$, done, $s_{t+1}$) 存到一个先进先出的 buffer 队列中。
- 当buffer满了后不断从 buffer 中随机抽样轨迹训练模型。
- 新模型产生的数据存入 buffer 中旧数据直接丢弃。
优先级经验回放:
主要思想:
帮助智能体学习如何做对的事而不是许多做错的事,回放内存中一些比其他经验信息量更大的经验,如果频繁使用信息量更大的经验则智能体会学的更快。
优先级经验回放主要实现了以下两个功能:
- 计算每个经验的优先级
- 根据优先级更新 buffer 并采取一个高效的采样策略采样轨迹。
经验优先度计算: 根据局部网络与目标网络的 TD 误差计算。
$TD_{error}= Q_{local}(s_t, a_t) - Q_{target}(s_t, a_t)$
TD 误差指出了当前的 Q值和下一步应该追求的 Q 值差距有多大,他表示当前经验有多么“令人惊讶”或“出乎意料”。
算法流程如下:
- 存储经验时为每个经验额外存储一个优先级($s_{t}$, $a_{t}$, $r_{t}$, done, $s_{t+1}$,$p$)
- 采样时按优先级比例对经验采样
- 计算每个经验的 TD 误差
- 使用 TD 误差更新 buffer 中经验优先级
算法优劣:
- 适用于 CPU 资源充足,奖励稀疏的场景
- 若奖励函数设计足够好则无需使用 PER,使用 PER 速度大大降低,性能不一定会提高。
Dueling-DQN
Dueling-DQN 对基础 DQN 网络结构做了修改,他将模型对未来奖励的总回报拆分成状态估计函数和优势估计函数两部分。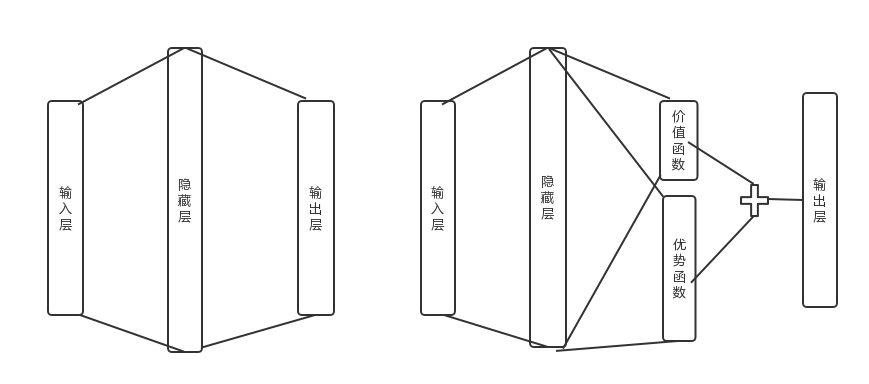
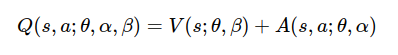
$V(s;\theta,\beta)$: 表示价值函数只针对当前的状态估计 Q 值不去考虑后续动作。
他的思想是:一个好的动作能将状态指向一个更有优势的局面,而不是任何时刻的动作都会影响状态的转移。
$A(s,a;\theta,\alpha)$: 是优势函数,意味着当前状态 s 下,某动作 a 相对于平均可用动作的优势。他量化了某一动作相对其他动作的好坏程度。
Dueling-DQN 与基础 DQN 区别:
- 基础 DQN 估计某一状态不同动作的 Q 值
- Dueling-DQN 只估计当前状态的 Q 值 + 某一动作的优势
DQN 算法学习 state 与每个离散动作一一对应的Q值后才能知道学到 state 的 Q 值,而 Dueling DQN 能通过优势函数直接学到 state 的价值,这使得 Dueling DQN 在一些 action 不影响环境的情况下能学比 DQN 更快。
D3QN(Dueling Double DQN)
Dueling DQN 与 Double DQN 结合,同时拆分动作选择与Q值计算。
Dueling DQN 与 Double DQN 相互兼容,并且是一个泛用性十分高的算法。